Buch 3

A Das Lennard-Jones-Modell und dessen Anwendung

1 Einführung

Selbst wenn man die genaueste Formel zur Berechnung von Molekülen hätte (z.B. 3d-Schrödinger), wäre sie vermutlich sehr aufwendig und daher für eine praktische Anwendung zu langsam.
Die im VDI-Wärmeatlas aufgeführten tabellierten Stoffdaten entstammen zwar Meßwerten, ihre praktische Anwendung ist jedoch ebenfalls zu langsam. 
Besser für die praktische Anwendung sind Daten in programmierter und leicht zugänglicher Form wie z.B. die Formeln der DIPPR Gesellschaft, welche in CHEMCAD enthalten sind.  

Mit der Lennard-Jones Gleichung lassen sich mit guter Näherung die Energiepotentiale zweier kugelförmiger Moleküle berechnen. Mit Hilfe der Summationskonstanten lassen sich die binären Potentiale auf ein Mol erweitern und u.a. die Bindungsenergie (s. 4.4) eines Stoffes berechnen. Siehe dazu auch Kap. 4.2. Grundsätzlich kann aus dem Potential eines Moleküls jede thermodynamische Größe hergeleitet werden.

Weitere Modelle sind Mie, Morse [Moelwyn-Hughes S. ] und Buckingham [Fleischhauer: Excel in Naturwissenschaft und Technik], s. Anhang.

Immerhin hat Kimball (Kap. B4) vermutlich als Einziger ein Atommodell erstellt, mit dem man die Bildung von Molekülen herleiten kann. Christen hat dies am Beispiel des H₂ Moleküls in seinem Buch übernommen s. f). Schumacher hat dieses Modell erweitert Kimb. Eigenschaften wurden damit aber noch nicht berechnet

2 Literatur

a) Chemcad Prozeß-Simulation (DIPPR Stoffdaten, Dipolmoment)

b) VDI Wärmeatlas (Stoffdaten, Dipolmoment)

c) Moelwyn-Hughes: Physikalische Chemie (M.H., S. 165, 168, 174, 206, 292, 245)

d) Lüdecke: Thermodynamik (SRK: S.307)

e) Poling, Prausnitz: The Physical Properties of Gases and Liquids (S. 9.7, 11.6, B.1)

f) Christen: Grundlagen der allgemeinen und anorganischen Chemie (Kimball Modell S. 25, 64)

g) D'Ans Lax, Band 2 und 3 (Brechungsindex, s. Kap. 4.2)

h) Ebert, Ederer (S. 100, 110)

i) Organikum (Brechungsindex s. Kap. 4.2)

j) CRC Handbook of Chemistry and Physics (Brechungsindex)

k) Wang, Schmidt; Berechnung von Stoffdaten und Phasengleichgewichten mit Excel und VBA (Atommodell S. 72)

3 Lennard-Jones Geichungen

Bekannt sind 2 Formen der Lennard-Jones Gleichung:

a)  die Gleichung von Mie 

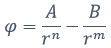
darin ist A der Abstoßungskoeffizient und B der Anziehungskoeffizient mit n = 12, m = 6.

b)  die allgemein verwendete Gleichung

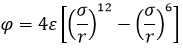
A, B, n, m, σ [Å] und ɛ aus ɛ/k [K] mit k, der Boltzmann Konstante sind Stoffkonstanten, r ist der Abstand beider Moleküle [Å]. φ ist das Energiepotenzial in den Einheiten von ɛ, d.h. J oder erg. Der Exponent m = 6 lässt sich nach Coulomb herleiten (Moelwyn-Hughes), der Exponent n = 12 ist empirisch. Die Koeffizienten σ [Å] und ɛ als ɛ/k [K] findet man u.a. in Poling, Prausnitz, sie lassen sich aber auch berechnen, wie nachstehend beschrieben ist.. σ ist der Abstand für φ  = 0.

Der Zusammenhang zwischen den Gleichungen 3a) und 3b) lasst sich mit folgenden Gleichungen beschreiben:

c)  

d)  damit berechnet man ε

e)

f)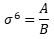

g)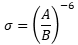 damit berechnet man σ

h) .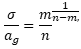 damit berechnet man a_g

a_g ist der Gleichgewichtsabstand.

 

Lennard-Jones Koeffizienten in Excel

Einfache Mischungsregel

i)

   

 

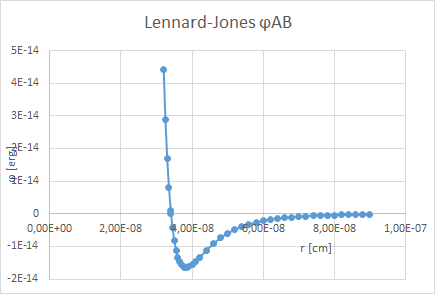
            Abb. 3b Lennard-Jones Potentialkurve

 

Bei φ = 0 wird r = σ. Bei φ = Minimum besteht Gleichgewicht und r = ag

4 Lennard-Jones Koeffizienten

Argon: ɛ/k_b = 93,3 K , σ = 3,542 Å aus 2e): S. B.1, A = 162E-105 [erg. cm¹²], B = 103,4E-60 [erg. cm⁶], aus 2c) S. 174}. ɛ = 1,288145517E-21 erg.

Mit der oben gezeigten Methode erhalten wir aus A und B die Daten σ = 3,4908E-08 und  ε = 1,6499E-18 erg

k_b = 1,380 649E-23 J/K = 1,380 649E-16 erg/K (Boltzmannkonstante)

1 Å = 10^-8 cm

ɛ₀ = 8,854 187 8128E-12 As/(Vm)

4.1 Virialkoeffizient B

Eine neue Methode besteht darin, die Lennard-Jones Koeffizienten aus der SRK- Gleichung (Soave Redlich Kwong) mit Hilfe des zweiten Virialkoeffizienten B zu berechnen.

a) Rayleigh-Gleichung aus Moelwyn-Hughes S. 45 (Herleitung) und Ebert, Ederer S. 110 numerische  Berechnung des Integrals nach Simpson .

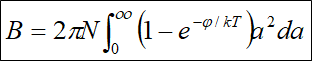
a = Molekülabstand, N = Avogadrozahl, k = Boltzmann Konstante.

und als neue Zustandsgleichung

b) 

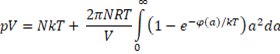
mit pV = p(V-b) und b, dem Eigenvolumen, erhält man eine Zustandsgleichung, die der van der Waals, PR, RK und SRK (Soave Redlich Kwong) Gleichung ähnlich ist, aber nicht empirisch, sondern analytisch hergeleitet ist.

Für φ wird in die Rayleigh Gleichung die Lennard-Jones Gleichung 3a eingesetzt. Die Integration erfolgt in VBA numerisch nach Simpson.

Rayleigh-Gleichung in Excel

c) B aus Zustandsgleichng SRK (Soave Redlich Kwong)

Z = 1 + B/V führt zu B = V(Z-1)

mit V = 22,71 l/mol bei 1 bar statt 1 atm

d) Vergleich beider Virialkoeffizienten a) und b)

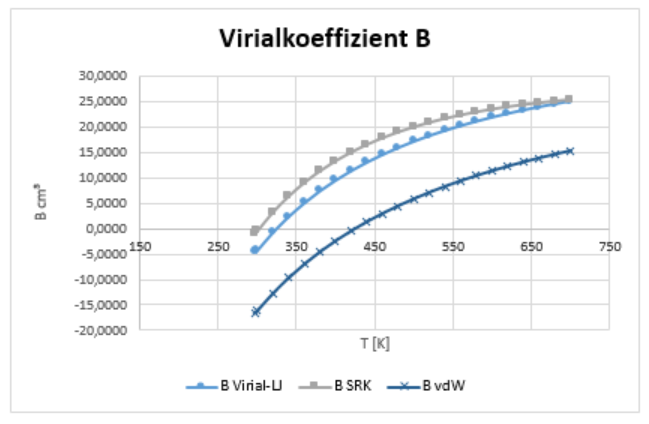
Abb. 4.1c Virialkoeffizienten für Stickstoff N₂ als Temperaturfunktion nach SRK (oben), Rayleigh (Mitte) und van der Waals (unten)

In der Virialgleichung nach Rayleigh wurden die Lennard-Jones Daten mit σ = 3,698 Å und ɛ/k = 95,05 K aus Ebert, Ederer, S. 113 verwendet.

e) Anpassung

Mit Hilfe der Excel Solver Funktion werden die Koeffizienten σ und ɛ solange verändert, bis B der Rayleigh-Gleichung mit B der SRK-Gleichung übereinstimmt.

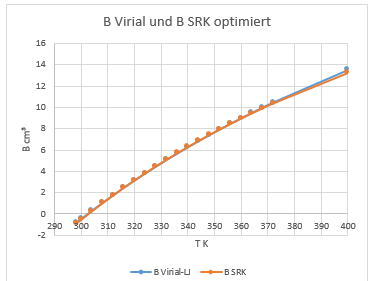
             Abb. 4.1d B für Rayleigh und SRK identisch

Damit erhält man für N₂ σ = 3,83 [Å] und ɛ/k 88;61 [K]. Die Daten in Poling, Prausnitz lauten σ = 3,69 [Å] und ɛ/k 71,4 [K].

f) Vergleich mehrerer kleiner Moleküle

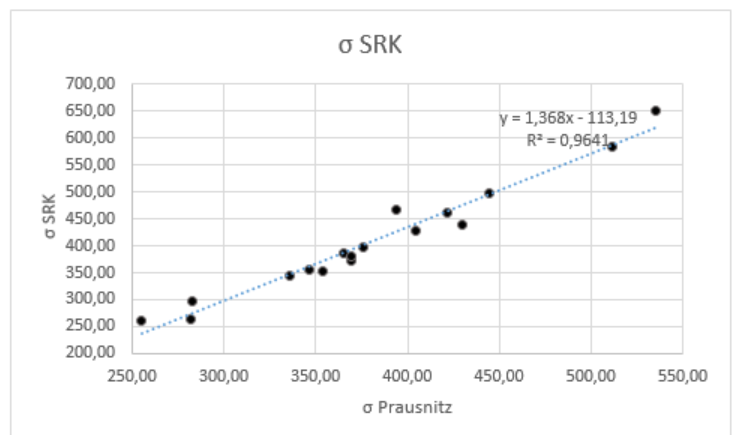
                  Abb. 4.1e-1 Vergleich σ Poling, Prausnitz mit σ SRK

Genauigkeit = 96,41%

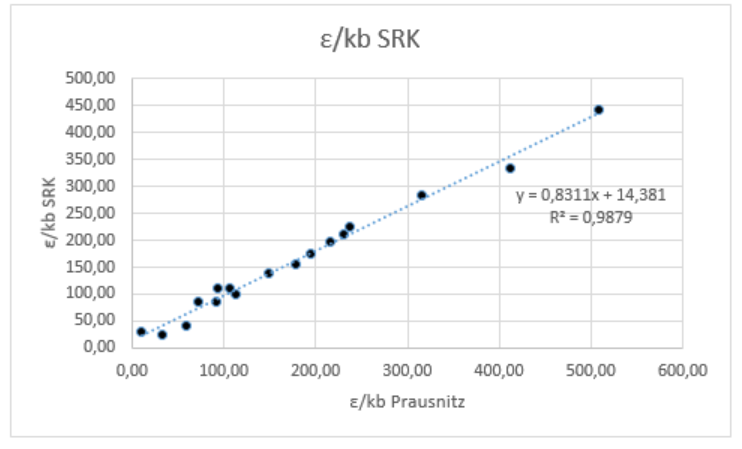
                  4.1e-2 Vergleich ɛ/k Poling, Prausnitz mit ɛ/k SRK

Genauigkeit = 98,79 %

 

4.2 Lennard-Jones Koeffizient B in Gleichung 3a

In der nachstehenden Form der Lennard-Jones Gleichung 3a

a)   

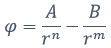
lässt sich der zweite Term nach Moelwyn-Hughes S. 245 aus der Summe von 3 Beziehungen berechnen. Diese sind die Dispersion, die Orientierung und die Induktion. Der Vorteil besteht u.a. darin, dass das Dipolmoment berücksichtigt wird, ansonsten aber wird nur die Molrefraktion benötigt, um daraus α und ν  zu berechnen, s. Moelwyn-Hughes S. 205. Dipolmomente findet man u.a. in CHEMCAD.

b)

c)

d)

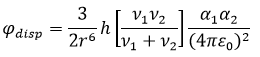
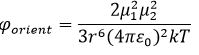
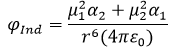
Darin sind α die Polarisierbarkeit [m³], ν die Bindungsfrequenz [s^-1] und µ das Dipolmoment [Cm] mit dem Planckschen Wirkungsquantum h, der Boltzmannkonstante k und der Dielektrizitätskonstante ε₀ (elektrische Feldkonstante). Diese Daten findet man u.a. in Physikalische Konstanten

In Moelwyn-Hughes S. 206 findet man Daten für diese 3 Gleichungen für etliche Stoffe. Wie leicht zu erkennen ist, erhält man über die beiden Indizes Potentiale für zwei unterschiedliche Stoffe wie z.B. Ethanol-Wasser. Bei der umfangreichen Herleitung der Formeln in c) M.H.wurde angenommen, dass die Moleküle frei rotieren können.

Aus der Molrefraktion R₀ lassen sich α und ν berechnen. R₀ wiederum kann aus Inkrementen, also Molekülgruppen ähnlich der Joback Methode, berechnet werden, s. M.H. S. 206. R₀ kann auich aus dem Brechungsindex berechnet werden, s,.c) M.H., g) D'Ans Lax und i) Organikum.

 

4.3 Lennard-Jones Koeffizienten aus kritischen Daten T_K und V_K

In Poling, Prausnitz S. 9.7 findet man folgende Gleichungen.

a) ɛ/k = T_K/1,2593

b) σ = 0,809 (V_K)^1/3

Darin sind Tk, die kritische Temperatur und ɛ/k in K, σ in Å, sowie Vk, das kritische Volumen in cm³/mol

Damit erhält man für Edelgase sowie kleine, unpolare Moleküle eine gute Näherungen.

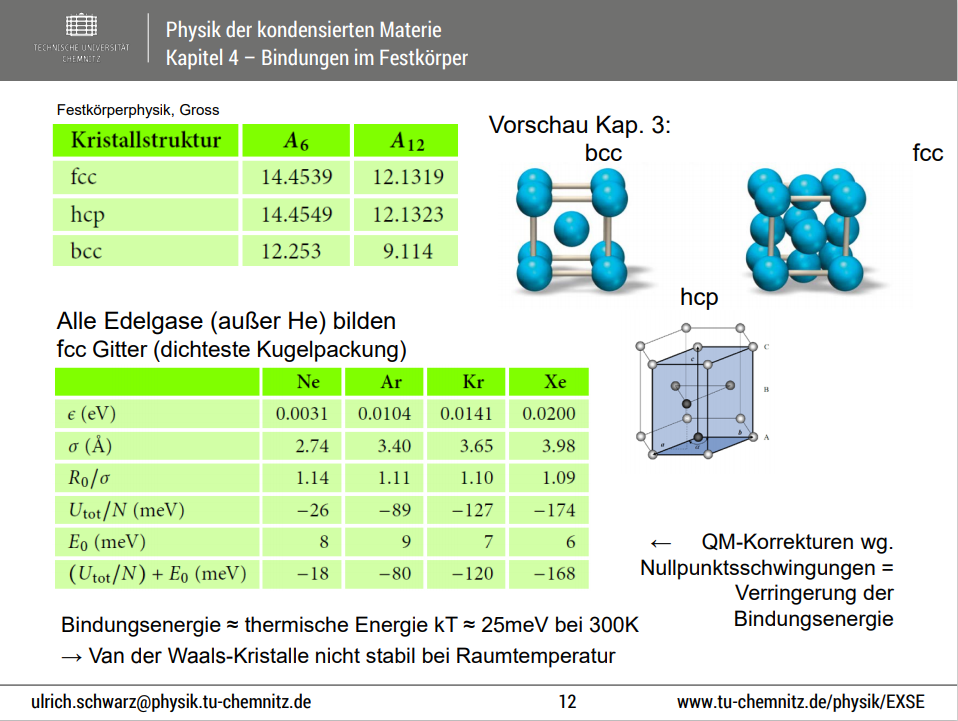
4.4 Summationskonstanten der Lennard-Jones Gleichung für Feststoffe

Die Summe aller binären Potentiale eines einzelnen Moleküls mit allen weiteren Molekülen berechnet man bei einem Kristall nach Moelwyn-Hughes S. 168 Gl. 41 mit dem Lennard-Jones Modell 3a wie folgt:

a) Moelwyn-Hughes S. 168 Gl. 41

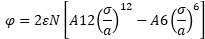
Darin sind c die Zahl unmittelbar benachbarter Moleküle und s_n und s_m die Summationskonstanten. N ist die Avogadrozahl = 6,022 140 76E23 mol-1 (Teilchen pro Mol).

Kubisch einfach: n = 12, m = 6, c = 6, s_n = 1,4002, s_m = 1,0337, A₆ = 8,402, A₁₂ = 6,201 (eigene Berechnung mit ca. 1 Million Moleküle in VBA).

Flächenzentriert bzw. hexagonal: n = 12, m = 6, c = 12, s_n = 1,0110, s_m = 1,2045, A₆= 14,4540, A₁₂ = 12,1320.

b) allgemeine Form, d.h. c ist in A₁₂ bzw. A₆ enthalten

Natürlich kann hier auch die Gl. 3b) verwendet werden.

In Tabelle 3 in M.-H. S. 168 findet man Daten für c und s_n und s_m.

Beispiel:  Bindungsenergie  und Daten zu A₆ und A₁₂.

4.5 Flüssigmodell

Nach Moelwyn-Hughes S. 159 nimmt man bei einer Flüssigkeit kleine geordnete Bereiche innerhalb weiter ungeordneter Gebiete an. Betrachtet man ein herausgegriffenes Molekül und seinen c unmittelbaren Nachbarn, erhält man die Lennard-Jones Gleichung:

a)

b) außerhalb dieses Raumes, d.h. r > a gilt

darin ist K eine Zahl und 

die Konzentration, mit a³ dem Volumen und κ, der reziproken Konzentration.

Die Integration ergibt

Darin ist c die Anzahl unmittelbarer Nachbarmoleküle analog einem Feststoff. Beim hexagonalen Kristall sowie beim flächenzentrierten Kristall ist c =12, beim kubischen Kristall nur 6. Außerhalb dieser Anordnung nimmt man eine homogene schalenförmige Struktur an. Die Zahl der Moleküle, die sich in einer Schale der Dicke dr in einem Abstand r von diesem Molekül befinden, ist 4πnr²dr, wobei n die Konzentration der Moleküle beträgt. Dann gilt für diesen Bereich

Bei einer Flüssigkeit gilt nach Moelwyn-Hughes S. 168 mit

c)

d)

e)

Für eine flächenzentrierte Anordnung, identisch mit hexagonal, erhält man mit c = 12, κ = 1/√2, n = 12, m = 6 und K = √2 s6 = 1,2198 und s12 = 1,0092. Die theoretischen Werte für das vollständige Kristall lauten: s6 = 1,2045 und s12 = 1,0110 (M.-H.), also sehr ähnlich. Bei einer kubischen Anordnung gilt c =  6, n = 12 und m = 6 und man erhält s6 = 1,3491 und s12 = 1,01454. Für ein kubisches Kristall gilt  s6 = 1,4003 und s12 = 1,0337 (M.-H.).

Diese Herleitung von M.-H. ist genial.  

 

4.6 Packungsdichte ρ

Die Packungsdichte ρ ist das Verhältnis atomares Kugelvolumen Vk /  Volumen Elementarzelle Ve. Bei dem einfachen kubischen Kristall ist das Kugelvolumen Vk = 4/3·π·r³ und das Volumen Elementarzelle
Ve = (2·r)³.

Daraus erhält man die Packungsdichte ρ für das einfache kubische Kristall ρ = Vk/Ve =  π/6 = 0,52360. Für die hexagonal dichteste Packung gilt auf die gleiche Weise ρ = √2·π/6 = 0,740480

Packungsdichte: Packungsdichte (Kristallographie) – Wikipedia (de.wikipedia.org/wiki/Packungsdichte_(Kristallographie))

 

B Wasserstoff Molekül aus 2 Wasserstoffatomen

1 Einführung

Das Potenzial zweier Wasserstoffatome setzt sich aus den Potenzialen Proton1-Proton2, Elektron1-Elektron2, Proton1-Elektron2 und -Proton2-Elektron1 zusammen. Daraus kann das Potential eines H₂ Moleküls berechnet werden.

Die in Christen hergeleitete Potentialfunktion lautet dann in atomaren Einheiten (ae)

Weitere Details s. Atomare Berechnungen

 

2 Literatur

a) Christen: Grundlagen der allgemeinen und anorganischen Chemie s. 2f)

b) Schumacher: kimb9 S. 12 (Herleitungen)

c) Tipler: Physik

d) Kimball Integral (Lösen aller Integral Gleichungen des Kimball Ansatzes)

e) Atomare Berechnungen (Herleitungen)

3 Kugelwolkenpotentiale

In eine homogen geladenen Kugel mit dem Radius 1,5 a₀ wird ein Proton aus dem Unendlichen bis zur Kugelmitte eingeführt, Darin ist a₀ der Radius eines Atoms.

Die Gleichung dazu lautet nach Tipler S.  904 und nach Schumacher S. 8

a)

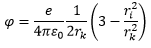
Darin ist r_i der Abstand des Protons vom Kugelmittelpunkt und r_k der Kugelradius .

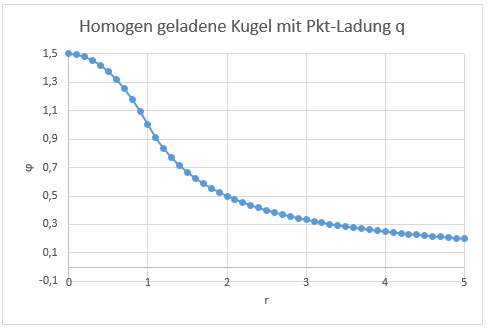
Abb. 3.1 Potenzial einer Punktladung (Proton) mit einer homogen geladenen kugelförmigen Elektronenwolke Radius R = 1,5 a₀

Überlappungspotential zweier homogen geladener Kugelwolken mit dem Radius a_0.

Schumacher S. 23ff

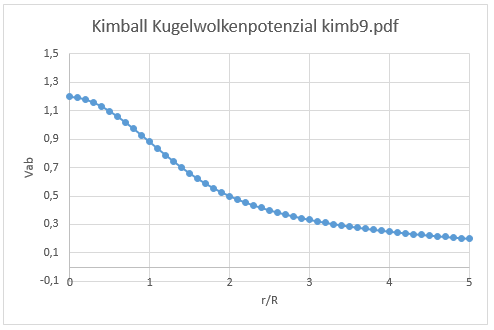
Abb 3.2 Überlappungs-Potenzial zweier homogen geladener kugelförmigen Elektronenwolken nach Kimball

Ist r = 0, lautet das Potenzial φ = 1,2. Diesen Wert erhält man auch, wenn man die totale Überlappung direkt berechnet, Schumacher S. 10-11

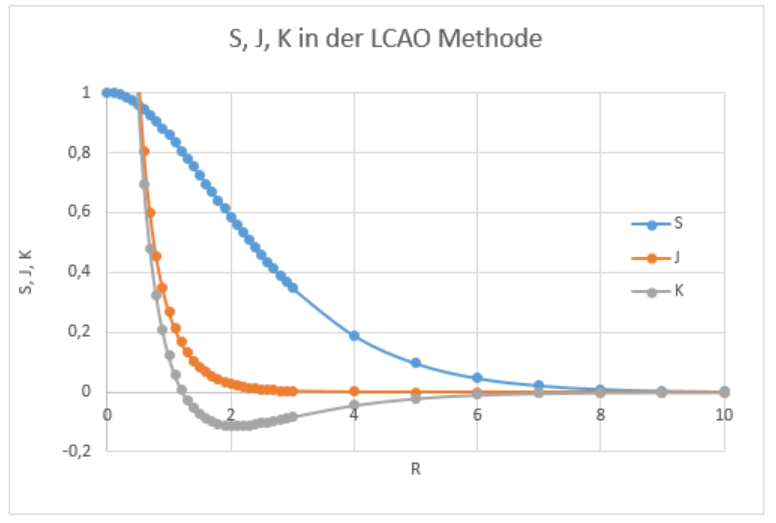
Abb. 3.3 Überlappungs-Potenziale der LCAO Methode (Herleitung nach TU Braunschweig Prof. Dr. Gericke)

Die blaue Kurve zeigt die Überlappung zweier Wasserstoff Elektronenwolken nach der Schrödinger Orbitaltheorie.Vergleicht man die blauen Kurven Abb. 3.2 mit 3.3, ist eine Ähnlichkeit zu erkennen. 

4 Berechnung der Verdampfungsenthalpie aus einer Zustandsgleichung

Am Beispiel der van der Waals und Redlich Kwong Gleichung wird die Verdampfungsenthalpie von Wasser auf der Basis thermodynamischer Funktionen berechnet

in Bearbeitung

C Anhang

1 Buckingham Potenzial

Die Buckingham Gleichung ist der Lennard-Jones Gleichung ähnlich. Die Buckingham Gleichung erlaubt die Berechnung atomarer Potenziale z.B. H-H, C-C und C-H.

Literatur: Fleischhauer: Excel in Naturwissenschaft und Technik.

Artikel: Buckingham Potenzial 

2 Beispiel: Wasser als 3D Modell

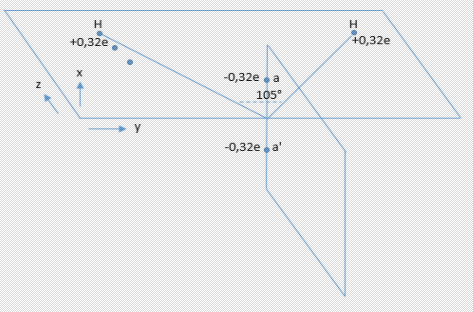
Abb. C2 Ladungsschwerpunkte von Wasser nach Rowlinson (Moelwyn-Hughes S. 263). Gemeinsam mit den Potenzialen der Protonen lassen sich leicht Coulomb Potenziale und van der Waals' sche Potenziale beliebiger Moleküle berechnen.

3 Atomare Daten s. Start

4 Sonstiges

Problem: Alle Eigenschaften von Molekülen lassen sich auf zwischenmolekulare Wechselwirkungen, sog. van der Waals-Potenziale zurückführen. Leider findet man dazu in der Literatur viel zu wenig. In der Praxis werden meist halbempirische Funktionen verwendet. Dies ist vermutlich darauf zurückzuführen, dass die Berechnungen sehr aufwendig und ohne entsprechende Programmierung nicht möglich sind. Dipolmomente: https://www.zum.de/Faecher/Materialien/beck/chemkurs/cs11-15.htm

https://www.amazon.com/Physikalische-Simulationen-mit-Personalcomputer-Quantenmechanik/dp/3662093332

 

Im hexagonalen hcp Kristall ist die Elementarzelle ein Tetraeder. Ebenso bilden viele Kohlenstoffverbindungen wie z.B. CH4 einen Tetraeder. Die Höhe h einer Tetraederfläche beträgt h = 0,5*wurzel(3) = 0,866025404, die Höhe des Tetraeders ist H = wurzel(2/3) = 0,816496581. Der Winkel des C-Atoms zu je 2 H-Atomen beträgt arccos(-1/3) = 109,47122064491