Atomare Daten
Ziel unseres 3. Buches ist die Berechnung von Stoffdaten auf der Basis atomarer Daten.
Die Wellenfunktion des Wasserstoffs nach Schrödinger und die Aufenthaltswahrscheinlichkeit des Elektrons.
Quelle: Hydrogen Ground State (hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydr.html)
Durch Integration von r = 0 bis unendlich erhält man den mittleren Atomradius einer mit 1e homogen geladenen Kugel für H = 1,5 *ao = 79,377 pm.
Wasserstoff H
Bohr'scher Radius a0= 0,529177E-10 m = 52,9177E-12 m = 52,9177 pm = 0,0529177 nm = 0,529177 Å
Atomradius (kovalent) = 37,2 pm, Bindungslänge = 74,4 pm (2*37,2), Energie = -13,6 eV nach Bohr und Kimball. Atomradius der homogenen Kugel nach Kimball = 79,377 pm, Bindungslänge (Proton-Proton) nach Kimball a = 71,9 pm (Christen S. 66)
van der Waals Radius r = 120 pm. 1 Å = 100 pm = 10-10 m. 1 pm = 10-12 m.
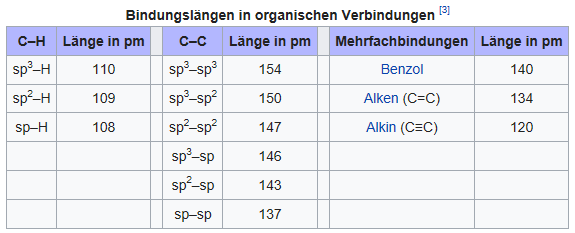
Quelle: https://de.wikipedia.org/wiki/Bindungslänge ³) Marye A. Fox, James K. Whitesell: Organische Chemie. Spektrum Akademischer Verlag, 1995, ISBN 3-86025-249-6.
Anm.: sp bedeutet Hybridisierung der s- und p-Orbitale.
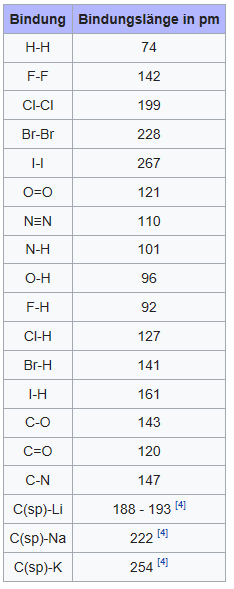
Quelle: https://de.wikipedia.org/wiki/Bindungslänge
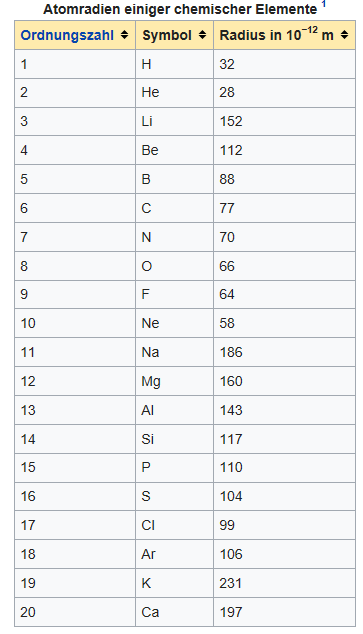
Quelle: https://de.wikipedia.org/wiki/Atomradius
C-C Bindung >C–C< (sp³-sp³)
Bindungslänge = 154 pm
Bindungswinkel = 109,47°, tetraedrisch
Ethen Doppelbindung >C=C< (sp³-sp²)
Bindungslänge = 134 pm
Bindungswinke = 120°, planar
Ethin Dreifachbindung –C≡C–
Bindungslänge = 120 pm
Bindungswinkel = 180 °, linear
C–H Bindung
sp³-H = 110 pm < (154 + 74,4) / 2 = 114,2
sp²-H = 109 pm > (134 + 74,4)/2 = 104,2
sp -H = 108 pm > (120 + 74,4)/2 = 97,2
C–O Bindung
Bindungslänge = 143 pm > (154 + 121)/2 = 137,5
C–N Bindung
Bindungslänge = 147 pm > (154 + 110)/2 = 132
OH-Gruppe
Bindungslänge = 96 pm < (121 + 74,4) = 97,7
Atomradien, Bindungslängen und Bindungsenergien nach Christen
Atomradien: H=30, C=77, N=70, O=66 pm
Bindungslängen: H2 =74, >C-C< =1,54, -N≡N- =1,094, O=O =1,207 pm
Tabelle1 Tabelle2 Tabelle3
Leybolds KaIottenmodell
https://de.wikipedia.org/wiki/Kalottenmodell
Das Kalottenmodell verwendet konstante Bindungsradien und konstante Wirkungsradien. Letztere beschreiben die Berührung der Moleküle einem Kristallmodell. Eine H-Kalotte sieht daher wie eine angeschnittene Kugel aus. Der Bindungsradius ist kleiner als der Wirkungsradius. Als Wirkungsradius kann der van der Waal'sche Radius (https://de.wikipedia.org/wiki/Van-der-Waals-Radius) verwendet werden.
Auszug aus https://de.wikipedia.org/wiki/Van-der-Waals-Radius. H hat danach einen van der Waals Radius von 110 pm
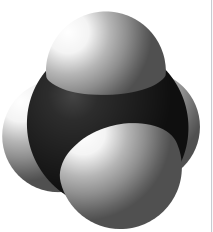
Kalottenmodell des Methans. Quelle: https://de.wiktionary.org/wiki/Methan
Das denkbar einfachste Molekülmodell könnte also dem Kalottenmodell nachempfunden werden.
Gittersummen nach Lennard-Jones:
Kubisch einfach scp: A6 = 8,4018, A12= 6,2015
Hexagonal fcc: A6 = 14,45489. A12 = 12,13229
Daten Quellen:
https://de.wikipedia.org/wiki/Bindungslänge
https://de.wikipedia.org/wiki/Bindungswinkel
http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/15/thc/bindung/tc022_h2plus.vlu/Page/vsc/de/ch/15/thc/bindung/bindungslaengen.vscml.html
Christen, H. Preuss
Literatur:
Atkins, Christen, Moelwyn-Hughes, Wedler
Berechnungen
Atomdurchmesser von Na und Cl aus der Dichte von NaCl:
MG = 58,4 g/mol, Dichte = 2,16 g/cm3, 1 Mol = 2 * 6,022*1023 Atome (Na + Cl). 58,4 g/mol / 2,16 g/cm³ = 27 cm3/mol.
Atomvolumen Na bzw. Cl: V = 27 cm3/ (2 * 6,022*1023 Atome (Na + Cl)) = 2,242*10-23 cm3.
Kubisch einfache Anordnung, d.h. würfelförmig. Aus V die 3. Wurzel ergibt: a = 282 pm. r = a/2 = 141 pm.
Der Ionenradius Na+ beträgt r = 102 pm, Cl- r = 181 pm, die Summe ist daher 283 pm.
(1 pm = 10-12 m), s. Tippler S. 1434.
------------------------------------------
Molekülvolumen Vm und Würfelkantenlänge eines Moleküls aus dem Molvolumen am Beispiel Wasser:
MG= 18 g/mol, Dichte= 1g/cm³, Molvolumen V= 18g/mol / 6,022E23 mol-1= 2,9893E-23 cm³.
Daraus 3. Wurzel ergibt a = 3,1E-8 cm (Kantenlänge eines Würfels), indem sich ein würfelförmiges Wassermolekül befindet. Die Größenordnung ist korrekt.
Andere Kristallformen wie z.B. kubischzentriert (bcc) oder flächenzentriert (fcc) ergeben ein geringeres Volumen, d.h. höhere Dichte. Hexagonal und flächenzentriert ist identisch bezüglich Volumen.
------------------------------------------
Abstoßungsexponent n bei Kochsalz nach Tipler S. 1433
r0 = 0,282 nm, k = 1/(4*pi*eps0) (Coulombkonstante)
Dissoziationsenergie (Epot) = 770 kcal/mol = 96,47 kJ/mol Ionenpaar =7,98 eV/Ionenpaar
Madelungzahl (Gittersumme): a = 1,7476
Epot = - a*k/r + A/r (Anziehung +Abstoßung)
dEpot/dr = 0 (Kräftegleichgewicht).
Ergebnis: r = r0
A = a*k*e2*r0(n-1/n)
n = 9,35
Potenziale
Parameter nach Buckingham, Lennard-Jones, Mie und Morse
Buckingham
Quelle: Fleischhauer: Excel in Naturwissenschaft und Technik, 2. Auflage
Lennard-Jones
http://www.csb.yale.edu/userguides/datamanip/autodock/html/Using_AutoDock_305.a.html
enthält atomare Lennard-Jones Parameter.
Poling, Prausnitz, O'Connell, The Properties of Gases and Liquids. Anhang B.1 Lennard-Jones Parameter
Mie
Quelle: Moelwyn Hughes: Physikalische Chemie, 1961
Morse
Quelle: Ebert, Ederer: Computeranwendungen in der Chemie, VCH 1985